Protein in electrolyte¶
Simulating a protein solvated in water and ions
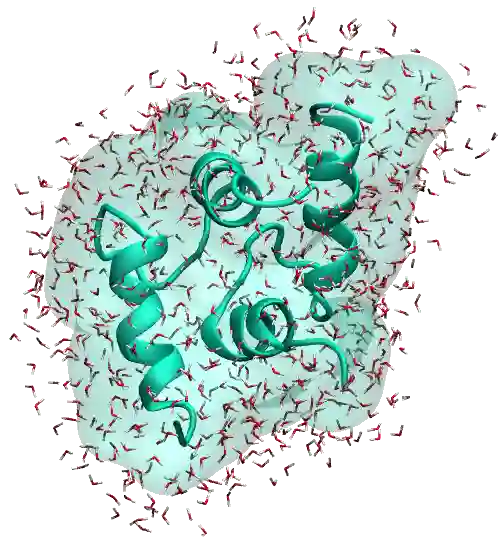

The goal of this tutorial is to use GROMACS and perform a simple molecular dynamics simulation of a protein solvated in an electrolyte. The protein is downloaded from the Protein Data Bank (PDB) [22] and solvated in an electrolyte made of water molecules and Na+ Cl- ions.
This tutorial covers some of the basic uses of GROMACS, including system preparation, force field selection, input file preparation, and data analysis.
If you are completely new to GROMACS, I recommend that you follow this tutorial on a simple Bulk salt solution first.
Struggling with your molecular simulations project?
Get guidance for your GROMACS simulations. Contact us for personalized advice for your project.
This tutorial is compatible with the 2024.2 GROMACS version.
Convert the PDB file¶
Download the .pdb file from the Protein Data Bank, or simply click here. The protein is a calcium-binding peptide from site III of chicken troponin-C that has been determined using 1H-NMR spectroscopy [23].
We first need to create the .gro file, i.e. a GROMACS structure file, from the .pdb file. This can be done using gmx trjconv:
gmx trjconv -f 1cta.pdb -s 1cta.pdb -o 1cta.gro -center -box 5 5 5
Choose the group System for the centering, and the group System as well for the output. A file named 1cta.gro is created. The generated .gro file contains 666 atoms, each atom corresponding to one line:
TROPONIN C SITE III - SITE III HOMODIMER
666
0ACE C 1 2.662 4.131 2.701
0ACE O 2 2.714 4.036 2.646
0ACE CH3 3 2.651 4.147 2.853
(...)
35NH2 HN2 664 2.417 3.671 3.192
69CA CA 665 3.016 2.279 1.785
70CA CA 666 1.859 2.046 1.838
5.00000 5.00000 5.00000
The last line is the box dimensions in nanometer, which was requested in the gmx trjconv command by the -box 5 5 5 option. All the options of trjconv can be found on the corresponding page of the GROMACS documentation.
Choose the force field¶
Let us select the force field that will control the interactions between the different atoms. This can be done using the gmx pdb2gmx command:
gmx pdb2gmx -f 1cta.gro -water spce -v -ignh -o unsolvated.gro
Here, the -ignh option is used to ignore the hydrogen atoms that are in the coordinate file. The -water spce open is used to specify the water model; the extended simple point charge model (spce) [24].
When running gmx pdb2gmx, choose the AMBER03 protein, nucleic AMBER94 force field [25]. A new gro file named unsolvated.gro was created, as well as a topology .top file named topol.top.
Solvate the protein¶
The protein is now ready to be solvated. Let us first immerse it in pure water using gmx solvate:
gmx solvate -cs spc216.gro -cp unsolvated.gro -o solvated.gro -p topol.top
Here, spc216.gro is a pre-equilibrated water configuration that is provided by GROMACS. After running gmx solvate, a number \(N = 3719\) of water molecules, or SOL (for solvent), is created in the new GRO file named solvated.gro next to the protein. The number \(N\) may slightly differ in your case. A new line must also appear at the end of the topol.top file:
(...)
[ molecules ]
; Compound #mols
Protein 1
SOL 3719
Run an energy minimization¶
Although gmx solvate creates molecules without overlap with the protein, it is safer to perform a short energy minimization to ensure that the distances between the atoms are reasonable.
To do so, create a new folder named inputs/, and create a file named mininimize.mdp into it. Copy the following lines into mininimize.mdp:
integrator = steep
nsteps = 50
nstxout = 10
cutoff-scheme = Verlet
nstlist = 10
ns_type = grid
couple-intramol = yes
vdw-type = Cut-off
rvdw = 1.0
coulombtype = pme
fourierspacing = 0.1
pme-order = 4
rcoulomb = 1.0
Here, the speepest-descent method is used, with a maximum number of steps of 50 [14]. The trajectory is printed every 10 step, as specified by the nstxout option. The other commands control the interactions and cut-offs.
Prepare the energy minimization using gmx grompp:
gmx grompp -f inputs/mininimize.mdp -c solvated.gro -p topol.top -o min -pp min -po min -maxwarn 1
gmx mdrun -v -deffnm min
The -maxwarn 1 is required here, because the system is not charge neutral and GROMACS will return a WARNING. The charge neutrality will be enforced later on. Finally, run the simulation using gmx mdrun:
gmx mdrun -v -deffnm min
Thanks to the steepest-descent algorithm, the potential energy of the system decreases rapidly and becomes large and negative, which is usually a good sign. The potential energy can be extracted using gmx energy:
gmx energy -f min.edr -o potential-energy-minimization.xvg
and choose Potential. The generated .xvg files contain the value of the potential energy (in kJ/mol) as a function of the simulation steps. The potential energy decreases from \(-3 \mathrm{e}-4~\text{kJ}/\text{mol}\) to \(-1.8 \mathrm{e}-5~\text{kJ}/\text{mol}\).
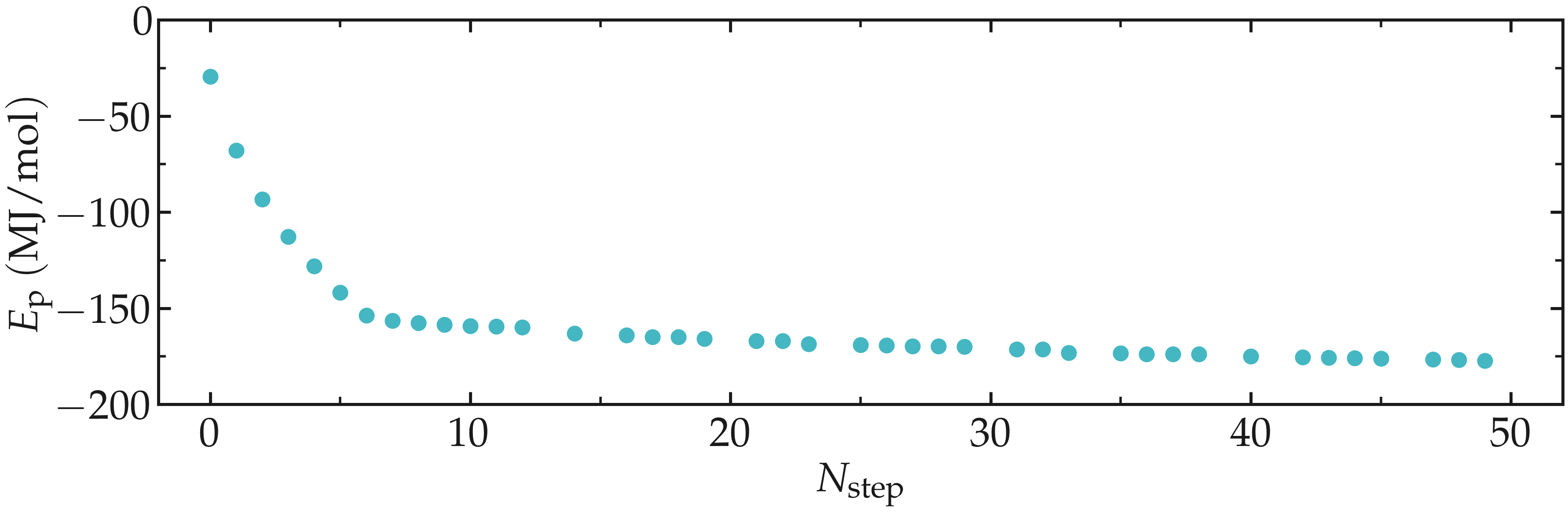
Figure: Potential energy \(E_\text{p}\) of the system as a function of the number of steps \(N_\text{step}\) during energy minimization.
Add the salt¶
Let us add some ions to the system so that the (1) total charge is 0, and (2) that the salt concentration is \(c_\text{s} \approx 1~\text{mol/L}\). This is done using the gmx genion command,
gmx genion -s min.tpr -p topol.top -conc 1 -neutral -o salted.gro
Select the group SOL as the continuous group of solvent molecules. GROMACS will replace some of the SOL residues with ions.
As can be seen from the topol.top file, some sodium (Na+) and chloride (Cl-) ions were added, and the number \(N\) of water molecules is reduced compared to the previous step:
[ molecules ]
; Compound #mols
Protein 1
SOL 3563
NA 81
CL 75
Out of safety, let us run a new energy minimization starting from the salted.gro configuration. The -maxwarn option is not necessary as the system is charge-neutral.
gmx grompp -f inputs/mininimize.mdp -c salted.gro -p topol.top -o min-s -pp min-s -po min-s
gmx mdrun -v -deffnm min-s
As previously, one can have a look at the potential energy using gmx energy:
gmx energy -f min-s.edr -o potential-energy-minimization-s.xvg
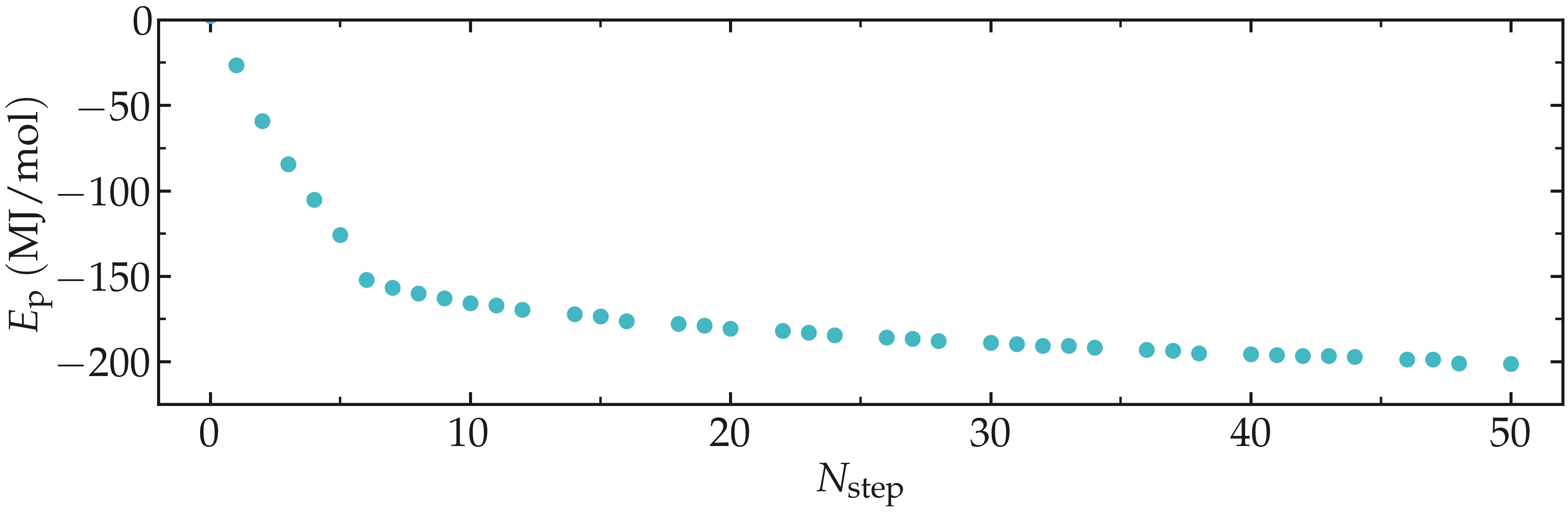
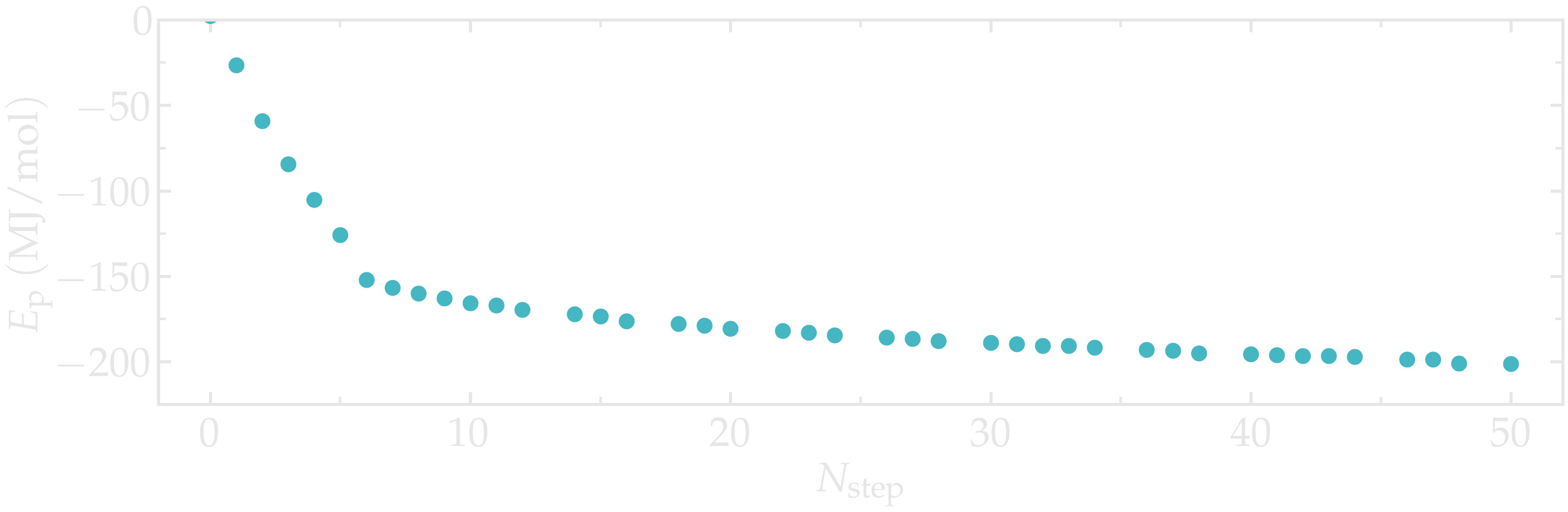
Figure: Potential energy \(E_\text{p}\) of the system as a function of the number of steps \(N_\text{step}\) during energy minimization.
The system can also be visualized using VMD using:
vmd min.gro min.trr
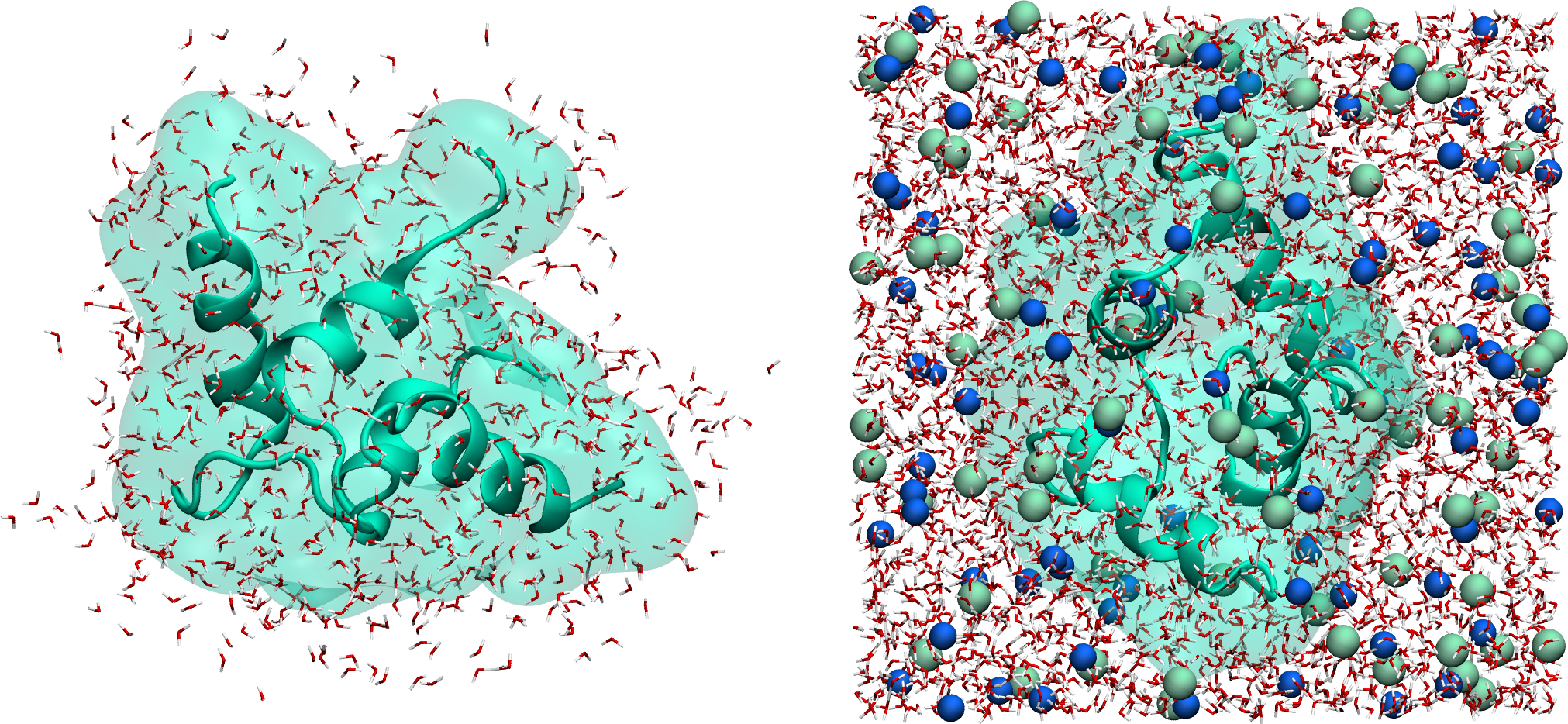
Figure: Protein solvated in water. On the left, only the water molecules that are near the protein are represented. On the right, the entire system is shown. Water molecules are represented as red and white sticks, and ions are represented as spheres.
Run the molecular dynamics¶
Create a new input file called nvt.mdp and placed into the inputs/ folder, and copy the following lines into it:
integrator = md
nsteps = 20000
dt = 0.001
comm_mode = linear
comm_grps = system
gen-vel = yes
gen-temp = 300
cutoff-scheme = Verlet
nstlist = 10
ns_type = grid
nstxout-compressed = 1000
vdw-type = Cut-off
rvdw = 1.0
couple-intramol = yes
coulombtype = pme
fourierspacing = 0.1
pme-order = 4
rcoulomb = 1.0
constraint-algorithm = lincs
constraints = hbonds
tcoupl = v-rescale
ld-seed = 48456
tc-grps = system
tau-t = 0.5
ref-t = 300
Here, the v-rescale thermostat is used to impose a temperature of \(T = 300~\text{K}\) with a characteristic time of \(0.5~\text{ps}\). The v-rescale thermostat corresponds to the Berendsen thermostat with an additional stochastic term [15], and is known to give proper canonical ensemble.
The LINCS algorithm is used to constrain the hydrogen bonds, allowing us to use a timestep of \(1~\text{fs}\). Without such constraint, the fast vibration of the hydrogen bonds would impose the use of a smaller timestep, which makes the computation more computationally expensive.
Run the NVT simulation:
gmx grompp -f inputs/nvt.mdp -c min-s.gro -p topol.top -o nvt -pp nvt -po nvt
gmx mdrun -v -deffnm nvt
Let us observe the potential energy. Let us also observe the temperature and the pressure of the system. Run the gmx energy command 3 times, and select successively potential, temperature, and pressure:
gmx energy -f nvt.edr -o potential-energy-nvt.xvg
gmx energy -f nvt.edr -o temperature-nvt.xvg
gmx energy -f nvt.edr -o pressure-nvt.xvg
After an initial spike, the energy, the temperature, and the pressure
all stabilize. For the temperature, the desired value of :math:`T = 300~\text{K}`
is reached, and for the pressure, a negative value of about :math:`- 700~\text{bar}`
can be observed.

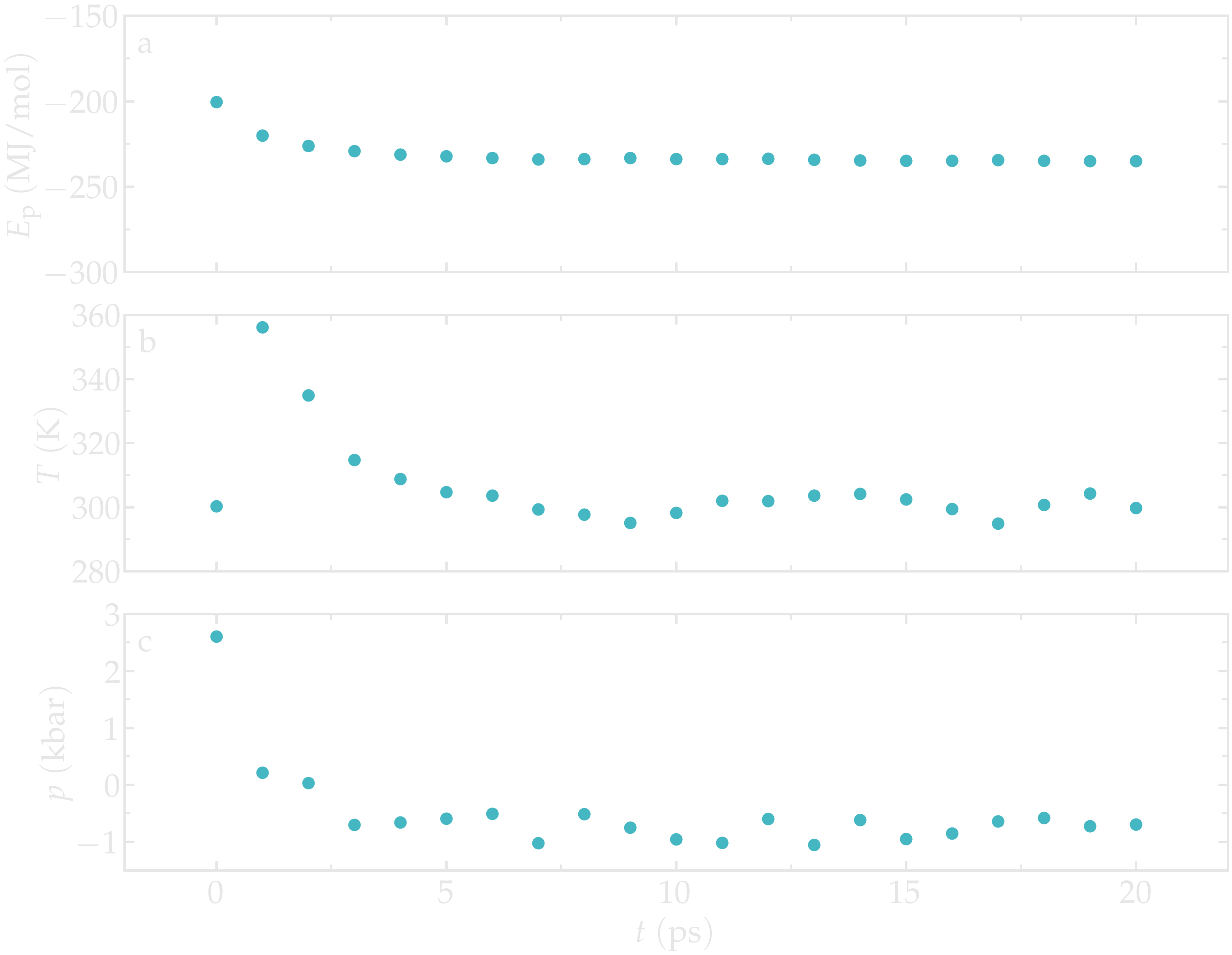
Figure: Potential energy \(E_\text{p}\) (a), temperature \(T\) (b), and pressure \(p\) (c) as a function of the time \(t\) during the NVT molecular dynamics.
The negative pressure indicates that the volume is slightly too large. This can be rectified by performing a short NPT simulation, during which the volume of the box will adjust until a desired pressure is reached. Create a new file called npt.mdp in the inputs/ folder. Copy the same lines as in nvt.mdp, and add the following lines to it:
pcoupl = c-rescale
Pcoupltype = isotropic
tau_p = 1.0
ref_p = 1.0
compressibility = 4.5e-5
Here, the isotropic c-rescale pressure coupling with a target pressure of 1 bar is used. Run it starting from the end of the previous nvt run:
gmx grompp -f inputs/npt.mdp -c nvt.gro -p topol.top -o npt -pp npt -po npt
gmx mdrun -v -deffnm npt
As the simulation progresses, the volume of the box decreases and better adjust to the fluid content of the box, as can be seen using gmx energy and extracting the volume, and/or by extracting the density:
gmx energy -f npt.edr -o volume-npt.xvg
gmx energy -f npt.edr -o density-npt.xvg
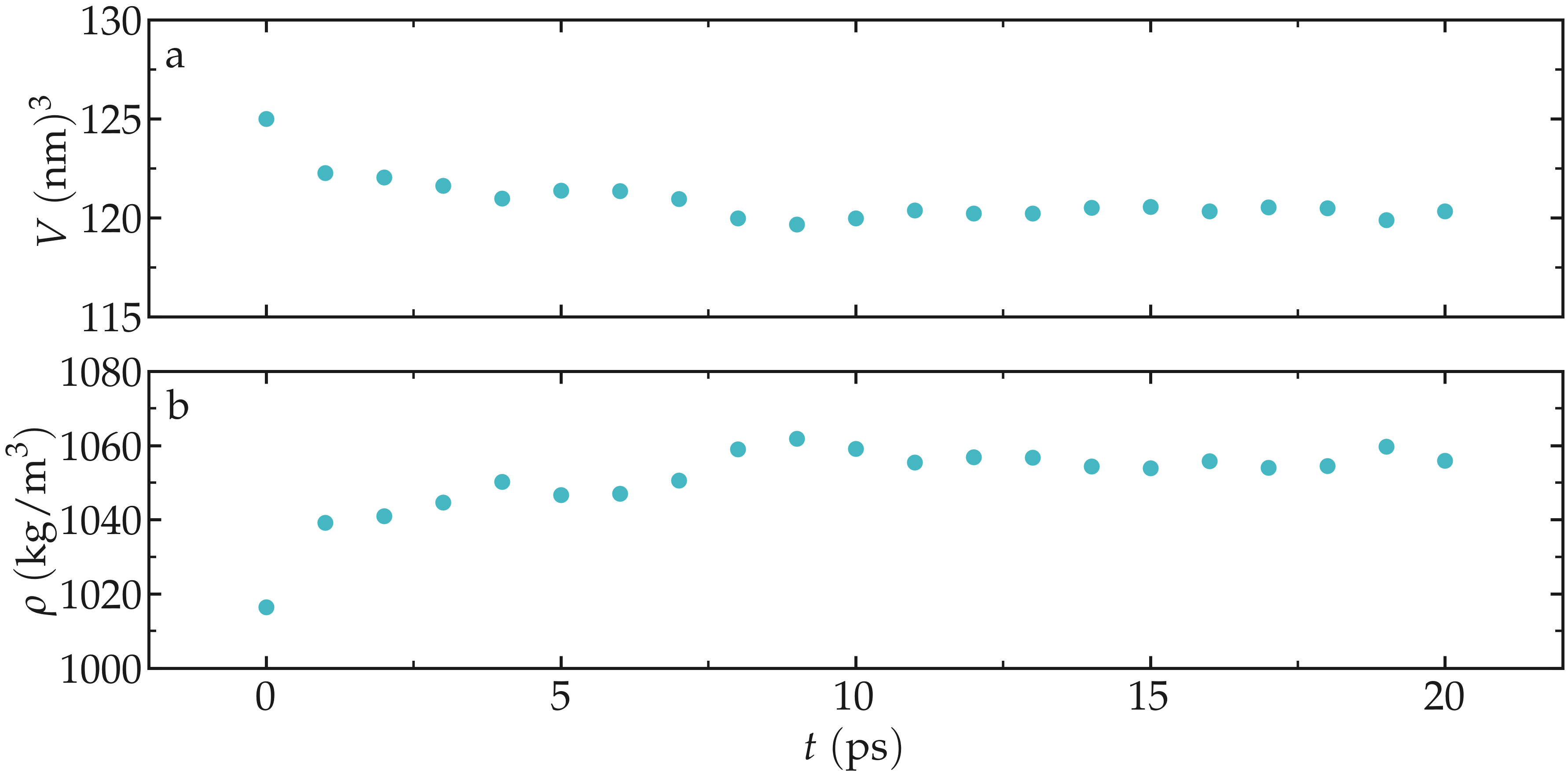
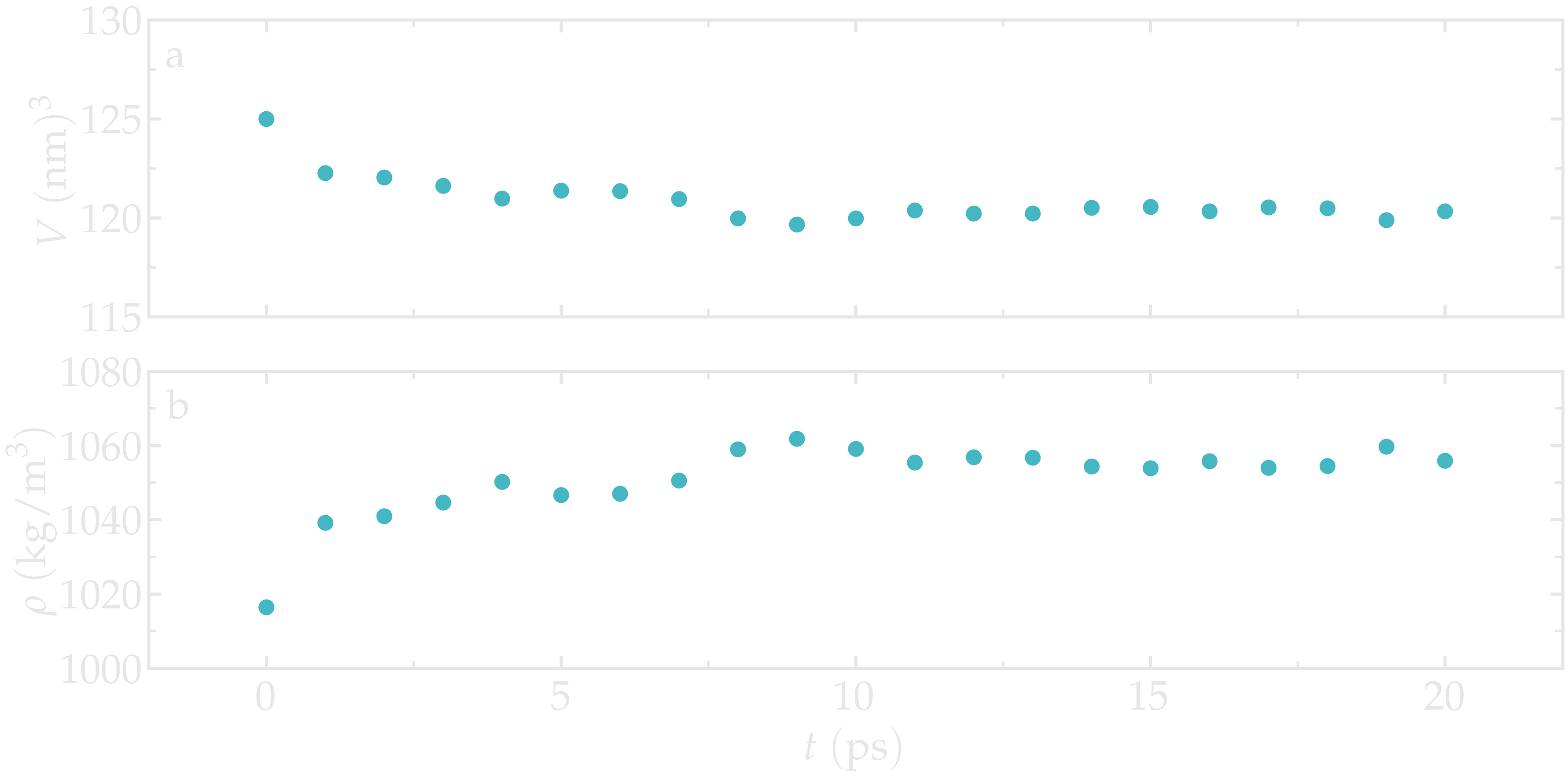
Figure: Box volume \(V\) (a) and density \(\rho\) (b) as a function of the time \(t\) during the NPT molecular dynamics.
You can access all the input scripts and data files that are used in these tutorials from GitHub.